dilluns, 19 de març del 2018
EXAMEN JCLIC!!!
dilluns, 12 de març del 2018
Transformació de moviment circular a alternatiu
Biela-manivella. Té dues barres articulades: una gira i l'altra es desplaça per una guia.
1.
La manovella gira de manera que la unió de la biela-manovella s'obre i empeny la barra.
2.
Quan la biela i la manovella estan alineades, la barra arriba al punt més distant.
3.
La manovella continua girant, la biela s'inclina i la barra retrocedeix.
4.
La biela retrocedeix fins que se superposa a la manovella i s'inverteix el moviment lineal.

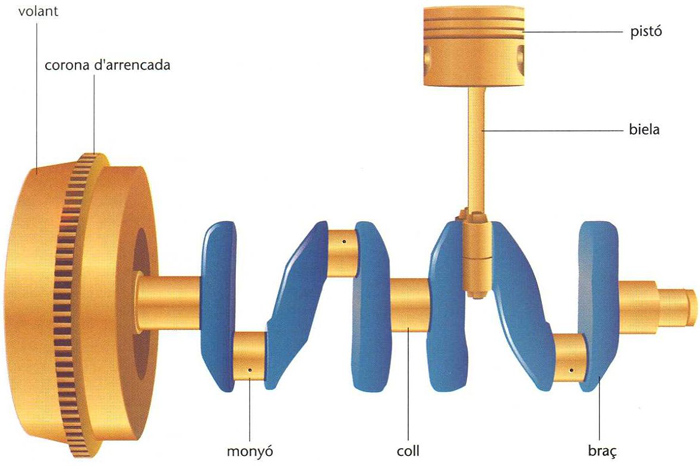
Excèntrica i cigonyal
Excèntrica. Transforma simultaniament un moviment de gir en diversos moviments alternatius.

Cigonyal. Transforma simultaneament un moviment de gir en diversos moviments alternatius.
1.
La manovella gira de manera que la unió de la biela-manovella s'obre i empeny la barra.
2.
Quan la biela i la manovella estan alineades, la barra arriba al punt més distant.
3.
La manovella continua girant, la biela s'inclina i la barra retrocedeix.
4.
La biela retrocedeix fins que se superposa a la manovella i s'inverteix el moviment lineal.

Excèntrica i cigonyal
Excèntrica. Transforma simultaniament un moviment de gir en diversos moviments alternatius.

Cigonyal. Transforma simultaneament un moviment de gir en diversos moviments alternatius.

dilluns, 5 de març del 2018
Transmissió per corretja
Transmissió per corretja
En aquest cas el mecanisme està format per una corretja que condueix el moviment d'una politja a una altra.

L'equació que relaciona el moviment de dues politges unides per una corretja és:
D1·W1=D2·W2
D1= diàmetre de la politja 1. W1= velocitat angular de la politja 1.
D2= diàmetre de la poltija 2. W2= velocitat angular de la poltija 2.
Transmissió per cadena i rodes
En aquest cas el mecanisme està format per una cadena i rodes dentades.

Es compleix l'equació d'equilibri de la transmissió per engranatges:
Z1·W1=Z2·W2
Z: nombre de dents.
W: velocitat angular.
Trens de mecanismes
Els trnes de mecanismes estan formats per la unió de diversos mecanismes simples.
Tren d'engranatjes
Si volem augmentar la velocitat d'un mecanisme, es fan servir diversos engranatges o politges acoblats, passant de l'engranatge més gros al més petit.

Tren de rodes i cadenes
Per unir un sistema de politges a un sistema d'engranatges cal que una politja i un engranatge estiguin en el mateix eix i girin a la mateixa velocitat; és a dir, que siguin solidaris.

Tren de politges
Per reduir la velocitat d'un motor podem unir diverses politges amb una corretja.

Cargol sense fi i roda
La unió d'un cargol sense fi amb una roda és una altra forma de transmissió de moviments, però aquest cop entre eixos que són perpendiculars entre ells.

En aquest cas el mecanisme està format per una corretja que condueix el moviment d'una politja a una altra.

L'equació que relaciona el moviment de dues politges unides per una corretja és:
D1·W1=D2·W2
D1= diàmetre de la politja 1. W1= velocitat angular de la politja 1.
D2= diàmetre de la poltija 2. W2= velocitat angular de la poltija 2.
Transmissió per cadena i rodes
En aquest cas el mecanisme està format per una cadena i rodes dentades.

Es compleix l'equació d'equilibri de la transmissió per engranatges:
Z1·W1=Z2·W2
Z: nombre de dents.
W: velocitat angular.
Trens de mecanismes
Els trnes de mecanismes estan formats per la unió de diversos mecanismes simples.
Tren d'engranatjes
Si volem augmentar la velocitat d'un mecanisme, es fan servir diversos engranatges o politges acoblats, passant de l'engranatge més gros al més petit.

Tren de rodes i cadenes
Per unir un sistema de politges a un sistema d'engranatges cal que una politja i un engranatge estiguin en el mateix eix i girin a la mateixa velocitat; és a dir, que siguin solidaris.

Tren de politges
Per reduir la velocitat d'un motor podem unir diverses politges amb una corretja.

Cargol sense fi i roda
La unió d'un cargol sense fi amb una roda és una altra forma de transmissió de moviments, però aquest cop entre eixos que són perpendiculars entre ells.

divendres, 2 de març del 2018
Ejercicios
1.- Se quiere obtener una rueda dentada receptora de 400rpm mediante un motor que tiene un engranaje en su eje de 80 dientes y que gira a 100rpm. Calcula el numero de dientes de la receptora.
Z1·400=80·100
Z1=80·100/400=20

2.- Dado el siguiente sistema de engranajes, calcula la velocidad de giro del engranaje 2 si el 1 gira a 10 revoluciones por segundo.
12·10=6·W2
120/6=W2
W2=20

3.- Se quiere construir un mecanismo multiplicador de velocidad con dos engranajes de 10 y 30 dientes respectivamente.
a) Indica cuál de ellos debe acoplarse al eje motor y cuál al conducido para conseguir la reducción de velocidad. La de 30.
b) Calcula la relación de transmisión. Cuando la de 30 da una vuelta la de 10 da 3.

Z1·400=80·100
Z1=80·100/400=20

2.- Dado el siguiente sistema de engranajes, calcula la velocidad de giro del engranaje 2 si el 1 gira a 10 revoluciones por segundo.
12·10=6·W2
120/6=W2
W2=20

3.- Se quiere construir un mecanismo multiplicador de velocidad con dos engranajes de 10 y 30 dientes respectivamente.
a) Indica cuál de ellos debe acoplarse al eje motor y cuál al conducido para conseguir la reducción de velocidad. La de 30.
b) Calcula la relación de transmisión. Cuando la de 30 da una vuelta la de 10 da 3.

Subscriure's a:
Comentaris (Atom)
